python手动计算信息增益

2019年5月23日 17:49 by wst

算法实践

---

概念阐述

对于决策树, 以前看了很多遍, 但是总感觉摸不着它.

里面有个很重要的概念: 信息增益. 

今天就来手动实现下, 实现之前先说下它的概念（这个定义里好多名词都有经验二字，是因为都是根据样本得到的）.

特征 A 对训练数据集D的信息增益 g(D,A) 定义为: 集合D的经验熵 H(D) 与特征A给定条件下D 的经验条件熵 H(D|A) 之差, 即:

                g(D,A) = H(D) - H(D|A)

通俗的说就是:  在一个条件给定情况下，信息不确定性减少的程度！

在决策树生成过程中,每次选择信息增益最大的那个特征作为节点.

举例说明

以买瓜为例, 夏天到了, 大家都比较爱吃西瓜, 但是怎么样才能买个好瓜呢? 要不然回家媳妇(女朋友)该说了, 你什么情况? 买个西瓜都买不好. 为了避免挨说, 还是得学好决策树, 搞清楚信息增益是怎么回事.

数据如下: (下载方式: 链接: https://pan.baidu.com/s/1Gr1TLaVwuwi9lO6BcdjoAQ 提取码: wr9j )

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

假设我们已经构建好了决策树，现在买了一个西瓜，它的特点是纹理是清晰，根蒂是硬挺的瓜，你来给我判断一下是好瓜还是坏瓜，恰好，你构建了一颗决策树，告诉他，没问题，我马上告诉你是好瓜，还是坏瓜？

根据决策树的算法步骤，我们可以得到下面的图示过程：

 

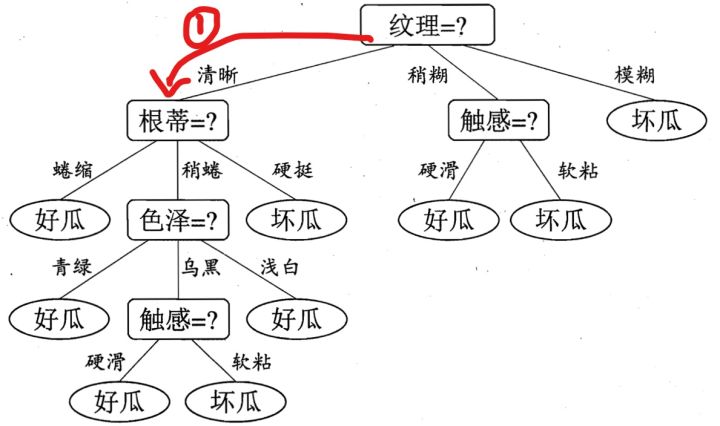
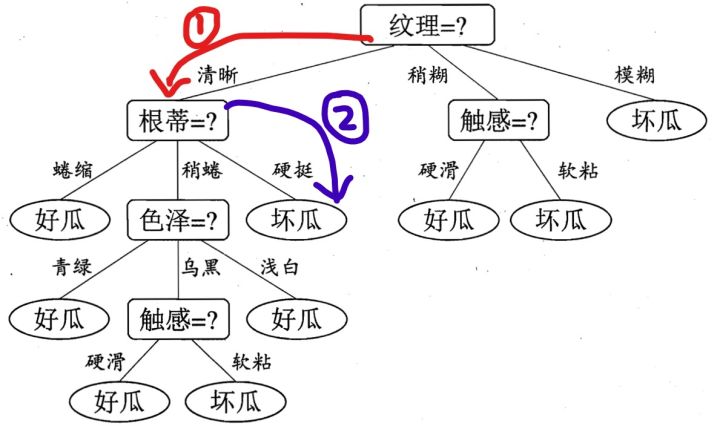
到达叶子结点后，从而得到结论。我这个瓜的判断是坏瓜（要挨说了）。

 

这里我们重点来说一下，在树每一层的生长过程中，如何选择特征！每一层选择好了特征之后，树也就自然建好了

第一个节点（每个节点都是如此）该怎么选呢?  根据我们的结论: 选择信息增益最大的那个特征作.

根节点下正例(好瓜)占 8/17，反例占 9/17 ，根结点的信息熵为

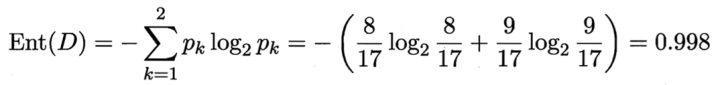
现在可选的特征有:{色泽，根蒂，敲声，纹理，脐部，触感}, 我们分别计算他们的信息增益:

色泽特征有3个可能的取值：{青绿，乌黑，浅白}

D1(色泽=青绿) = {1, 4, 6, 10, 13, 17}，正例 3/6，反例 3/6 -- 6,3,3

D2(色泽=乌黑) = {2, 3, 7, 8, 9, 15}，正例 4/6，反例 2/6 -- 6,4,2

D3(色泽=浅白) = {5, 11, 12, 14, 16}，正例 1/5，反例 4/5 -- 5,1,4

3 个分支结点的信息熵

 

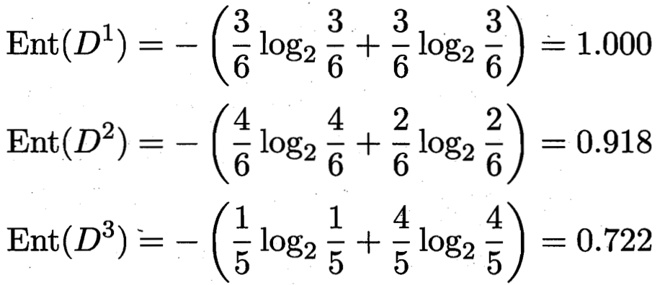
那么我们可以知道属性色泽的信息增益是：

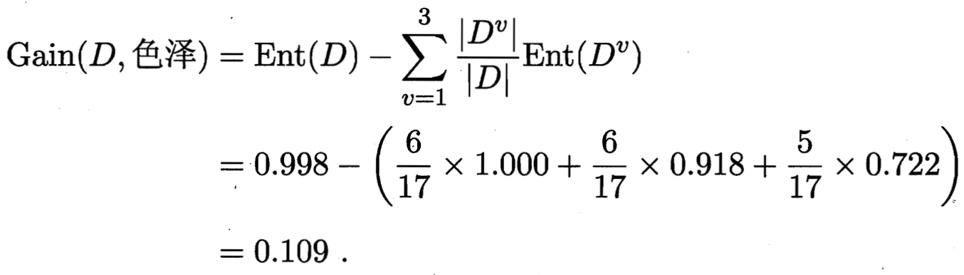
同理，我们可以求出其它属性的信息增益，分别如下：

根据后文的代码，计算过程为（里面的数字，通过excel筛选即可得到）：

# 色泽
In [21]: h(8,9,[[6,3,3],[6,4,2],[5,1,4]])
Out[21]: 0.10812516526536531
# 根蒂
In [22]: h(8,9,[[8,5,3],[7,3,4],[2,0,2]])
Out[22]: 0.14267495956679288
# 敲声
In [23]: h(8,9,[[5,2,3],[2,0,2],[10,6,4]])
Out[23]: 0.14078143361499584
# 纹理
In [24]: h(8,9,[[3,0,3],[9,7,2],[5,1,4]])
Out[24]: 0.3805918973682686
# 脐部
In [25]: h(8,9,[[7,5,2],[4,0,4],[6,3,3]])
Out[25]: 0.28915878284167895
# 触感
In [26]: h(8,9,[[5,2,3],[12,6,6]])
Out[26]: 0.006046489176565584

于是我们找到了信息增益最大的属性纹理，它的Gain(D，纹理) = 0.381最大。
于是我们选择的划分属性为“纹理”
如下：

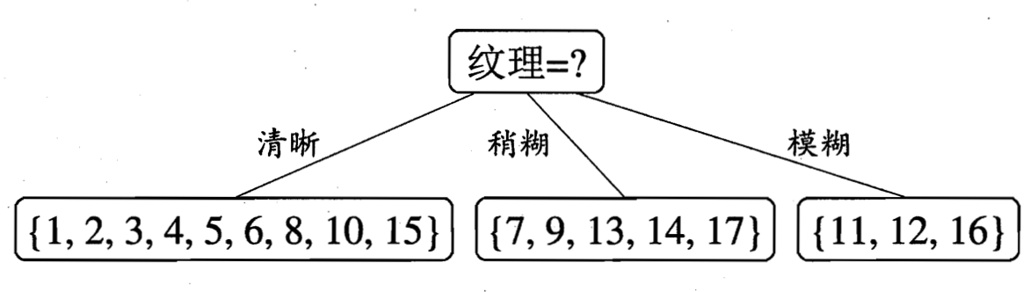于是，我们可以得到了三个子结点，对于这三个子节点，我们可以递归的使用刚刚找信息增益最大的方法进行选择特征属性，
比如：D1(纹理=清晰) = {1, 2, 3, 4, 5, 6, 8, 10, 15}，下次可选的属性集合{色泽、根蒂、敲声、脐部、触感}，基于 D1各属性的信息增益，分别求得如下：

手动编码计算:

In [1]: import pandas as pd

In [2]: import numpy as np

In [3]: import math

In [14]: def lg(v):
    ...:     if v==0:
    ...:         return 0
    ...:     return -v*math.log(v,2)
    ...: 
    ...: 

In [15]: def h(f_1, f_0, matrix):
    ...:     a = f_1+f_0
    ...:     d = lg(f_1/a) + lg(f_0/a)
    ...:     m = 0
    ...:     for lis in matrix:
    ...:         m += lis[0]/a * (lg(lis[1]/lis[0]) + lg(lis[2]/lis[0]))
    ...:     return d-m
    ...: 
    ...:     

In [16]: h(7,2,[[4,3,1],[4,3,1],[1,1,0]])
Out[16]: 0.04306839587828004

In [17]: h(7,2,[[5,5,0],[3,2,1],[1,0,1]])
Out[17]: 0.45810589515712374

In [18]: h(7,2,[[2,2,0],[1,0,1],[6,5,1]])
Out[18]: 0.33085622540971754

In [19]: h(7,2,[[5,5,0],[1,0,1],[3,2,1]])
Out[19]: 0.45810589515712374

In [20]: h(7,2,[[3,1,2],[6,6,0]])
Out[20]: 0.45810589515712374

代码说明:

f_1 -- 好瓜个数, f_0 -- 坏瓜个数, matrix -- 里面有多行, 每一行代表一个属性值的情况: 此属性值个数、此属性值下好瓜的个数、此属性值下坏瓜的个数。

比如色泽属性，在纹理清晰的情况下，有7个好瓜，2个坏瓜。同时：

色泽青绿的有4个，这4个中有3个好瓜、1个坏瓜；

色泽乌黑的有4个，这4个中有3个好瓜、1个坏瓜；

色泽浅白的有1个，这1个是好瓜；

此时matrix为:

[ [4, 3, 1],

[4, 3, 1],

[1, 1, 0]]

函数调用方式为：h(7,2,[[4,3,1],[4,3,1],[1,1,0]])， 值为0.043

同理，可以算出来根蒂的信息增益为：0.458；敲声：0.331，脐部：0.458，触感：0.458 

 

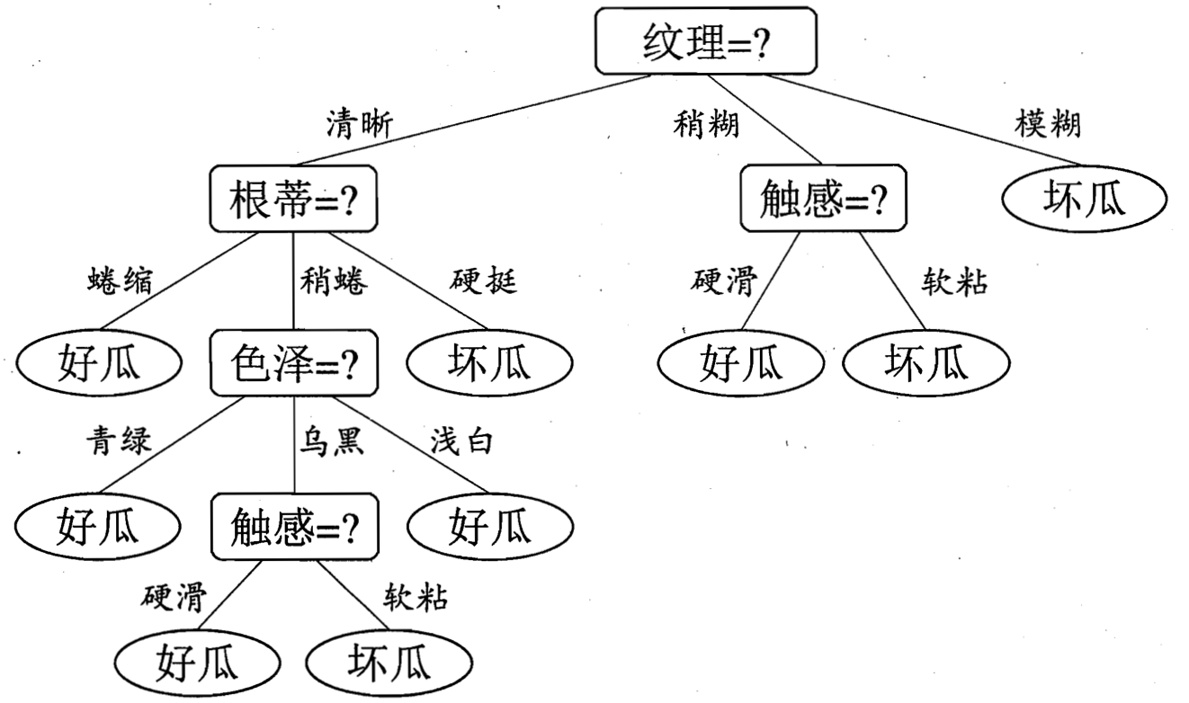
于是我们可以选择特征属性为根蒂，脐部，触感三个特征属性中任选一个（因为他们三个相等并最大），其它俩个子结点同理，然后得到新一层的结点，再递归的由信息增益进行构建树即可
我们最终的决策树如下：

 

参考：

作者：忆臻

链接：https://www.zhihu.com/question/22104055/answer/161415527

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

---